Warehouse Math

Digital Twins, which are virtual replicas of physical assets, are increasingly being used in e-commerce warehouse management to enhance efficiency and decision-making (Bélanger et al., 2023). One key use case is inventory management optimization, where Digital Twins enable real-time tracking of stock levels and help optimize storage layouts. This reduces the risk of overstocking or stockouts, leading to more efficient use of space and better order fulfillment.

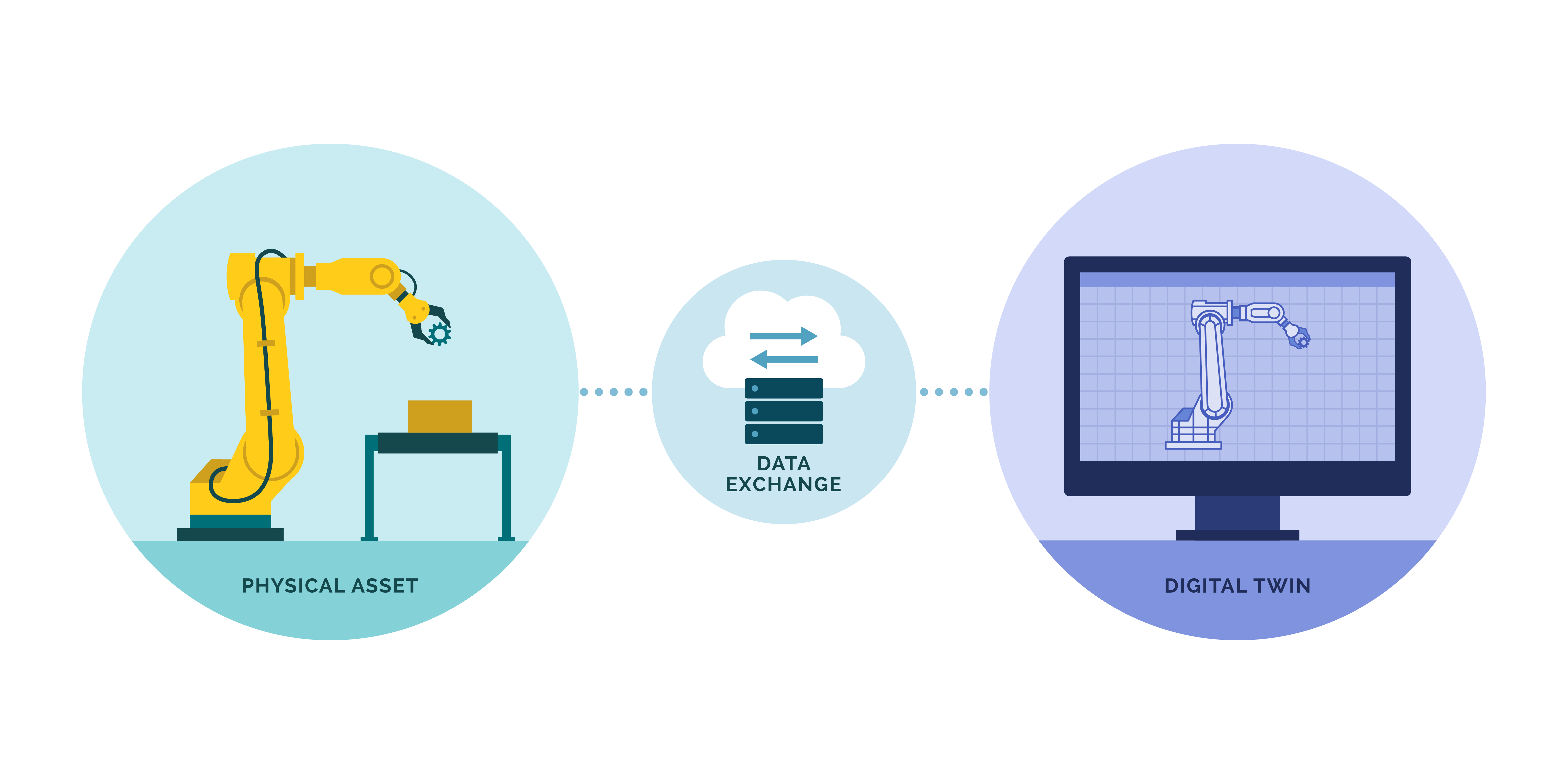
Another significant application is predictive maintenance. By monitoring equipment health and simulating various conditions, Digital Twins can predict machinery failures before they happen, allowing for proactive maintenance that minimizes downtime and extends equipment lifespan.

Operational efficiency is also improved through Digital Twins, as they can simulate warehouse processes like picking and packing. This helps identify and eliminate bottlenecks, optimize workflows, and improve labor allocation without disrupting ongoing operations.

In terms of safety, Digital Twins play a crucial role by simulating potential hazards and ensuring compliance with safety regulations. They also assist in testing emergency protocols and training staff using virtual models, thereby reducing risks in high-stakes environments.

And above all, Digital Twins contribute to sustainability efforts by providing insights into energy consumption and waste management. This allows companies to optimize their energy use, reducing both their carbon footprint and operational costs.

Use Case: Amazon Warehouse

Amazon Robotics has leveraged NVIDIA Omniverse digital twin technology to simulate and optimize warehouse operations. These digital twins improve efficiency, safety, and security by modeling and predicting various scenarios. They are used to optimize space utilization, automate tasks like picking and packing, and enhance safety protocols, such as ergonomics and fire prevention. Additionally, digital twins assist in planning and validating warehouse layouts, traffic flows, and emergency response strategies.

Warehouse Math

For developing a digital twin for an e-commerce warehouse, the first and critical step is to formulate a mathematical model of the warehouse’s operations. This model would include the layout of storage areas, the movement of goods, order fulfillment processes, inventory levels, and logistics flows. By representing these elements mathematically, the model can simulate the warehouse’s behavior under various scenarios, such as peak shopping seasons or changes in demand. This allows for real-time monitoring, optimization of warehouse processes, and predictive analysis to anticipate bottlenecks or inefficiencies. An accurate mathematical model ensures that the digital twin can provide actionable insights to improve operational efficiency, reduce costs, and enhance customer satisfaction.

To formally describe an e-commerce warehouse suitable for building a digital twin, it is essential to represent the key components and processes algebraically, as in the following.

Warehouse Layout and Space Representation

Let \( W \) be the warehouse space, divided into \( N \) storage units or locations. Each storage location \( S_i \) (where \( i \in {1, 2, \dots, N} \)) can hold a certain quantity of items \( Q_i(t) \) at time \( t \).

The total space capacity \( C_i \) of each storage location \( S_i \) must be

\[Q_i(t) \leq C_i\]

This constraint ensures that the inventory at any storage location does not exceed its capacity.

Inventory Management

Let \( I_j(t) \) represent the inventory level of item \( j \) at time \( t \), where \( j \in {1, 2, \dots, M} \) and \( M \) is the total number of different items. The relationship between items and storage locations can be modeled as

\[Q_i(t) = \sum_{j} x_{ij} \cdot I_j(t)\]

where \( x_{ij} \) is a binary variable indicating whether item \( j \) is stored in location \( i \) (1 if yes, 0 if no).

Order Fulfillment Process

Let \( O_k(t) \) represent the order \( k \) to be fulfilled at time \( t \), where \( k \in {1, 2, \dots, K} \) and \( K \) is the total number of orders. Each order \( O_k(t) \) is a vector

\[O_k(t) = [o_{k1}(t), o_{k2}(t), \dots, o_{kM}(t)]\]

where \( o_{kj}(t) \) indicates the quantity of item \( j \) requested in order \( k \) at time \( t \).

The fulfillment of order \( O_k(t) \) requires retrieving items from storage:

\[F_k(t) = \sum_{i} y_{ik} \cdot Q_i(t)\]

where \( y_{ik} \) is a binary variable indicating whether storage location \( i \) is involved in fulfilling order \( k \).

Logistics and Movement

Let \( R(t) \) represent the set of routes or paths taken by retrieval units (e.g., robots, human pickers) at time \( t \). Each route \( r_i(t) \) for retrieval from storage location \( S_i \) to the packing area has a time \( T_i(t) \) and distance \( D_i(t) \) associated with it, which can be minimized by optimizing \( R(t) \). The total retrieval time \( T_{\text{total}}(t) \) for all orders can be expressed as

\[T_{\text{total}}(t) = \sum_{i=1}^{N} T_i(t) \cdot \sum_{k=1}^{K} y_{ik}\]

Dynamic Replenishment

Replenishment of inventory is modeled as \( R_j(t) \) for item \( j \) at time \( t \), where \( R_j(t) \) adds to the inventory:

\[I_j(t+1) = I_j(t) + R_j(t)\]

Replenishment is triggered based on a threshold \( T_j \), where \( R_j(t) > 0 \) if \( I_j(t) < T_j \).

Demand Forecasting and Optimization

Let \( D_j(t) \) represent the forecasted demand for item \( j \) at time \( t \). Inventory levels are optimized by minimizing the cost function

\[C(t) = \sum_{j=1}^{M} \left[ h_j \cdot I_j(t) + p_j \cdot (D_j(t) - I_j(t))^2 \right]\]

where \( h_j \) is the holding cost and \( p_j \) is the penalty cost for stockouts.

Performance Metrics

Throughput \( T_{\text{p}}(t) \): The rate at which orders are fulfilled, modeled as

\[T_{\text{p}}(t) = \frac{1}{K} \sum_{k=1}^{K} \frac{1}{T_{\text{total}}(t)}\]

Utilization \( U(t) \): The proportion of warehouse space used, calculated as

\[U(t) = \frac{\sum_{i=1}^{N} Q_i(t)}{\sum_{i=1}^{N} C_i}\]

This mathematical description can be used to build a digital twin by translating these equations and variables into simulations, which can then be dynamically updated with real-time data from the warehouse to monitor and optimize its operations.

Omniverse Workflow

The workflow for developing a digital twin of an e-commerce warehouse on Nvidia Omniverse involves several steps.

The process begins with defining the 3D environment using tools like Autodesk Maya or the open-source Blender, where all elements of the warehouse are modeled before being imported into Omniverse. The 3D warehouse model can be imported into Nvidia Omniverse using connectors or USD (Universal Scene Description) files.

Within Omniverse, the mathematical models are scripted using Python to simulate essential processes such as inventory management, order fulfillment, and logistics. For example, each storage location \( S_i \) is represented as an object in the scene with an associated property \( Q_i(t) \) for inventory level.

Real-time data feeds from the physical warehouse must then be integrated, allowing the digital twin to get dynamically updated with current information. AI models for forecasting and optimization are implemented, with their inferences feeding back into the simulation to refine operations. The warehouse operations are visualized in real-time, with parameters adjusted as needed to optimize performance based on the simulation results.

Interactive dashboards within Omniverse can be built to visualize key metrics such as throughput \( T_{\text{p}}(t) \), utilization \( U(t) \), and real-time inventory levels.